The one where hexes are indexed
This post walks through how to index a pixel based hex grid in Love2D using Fennel. The concepts presented here should carry over into other frameworks and will work with other languages.
Red Blog Games has a great step by step tutorial on how to work with regular hexagons. I’ve used the approach presented in this blog post before on my previous game Frozen Horizon. It worked wonderfully with the SVG based graphics.
In my most recent strategy Game Gnomic Vengeance, I used pixel art hexagons. Due to their inherent design, pixel art hexagons aren’t regular, meaning that nice efficient indexing algorithms wont work.
Here I present the my approach to working with irregular pixel art hexagons, adapted from Red Blog Games implementation example.
Mapping Mouse Position to a Hexagon Grid Using Pixel Values
One way of mapping mouse position to in game objects is to use a reference image. The reference image renders an object’s selectable geometry in one solid colour. The colour is associated with the object’s unique id. Rather than rendering this reference image, its used to get the object id under the mouse during the update cycle.
Expanding this concept to the hexgrid, if we give each hexagon on the grid a unique colour, we can identify the hexagon our cursor is over using the pixel value of the reference image.
In the example reference image below, we use the red channel to indicate the x value and the green channel to indicate the y value. As the player’s cursor moves over the image the red and green values would be checked each frame to get the x and y position of the hexagon in the hexgrid.

The limitation with this approach is that as the size of the hexagon grid increases, so to does the image needed to index it. There are workarounds for this, such as rendering our reference image onto a smaller canvas or doing an initial wide search and creating a new reference image each frame that only renders the area immediately around the mouse. These trade off precision, in the case of the scaled down image, and processing cost, in the case where an initial wide search is performed.
What we need is some geometry that can be efficiently indexed and that tiles a fixed reference image over the hexgrid.
Identifying a Super-tiling Rectangle
Hexagons can be super-tiled by a rectangle that is a function of the hexagon size. There are many super-tiling rectangles to choose from. For the purpose of this example I am using one that is twice the width of the hex and twice the height. If this rectangle is staggered with respect to the y index, it will tile cleanly over the hexagons.

The reference image is now fixed in size and requires far fewer colour values to represent the position of the cursor. The rectangle I chose contains parts of 6 hexagons. Other rectangles can be used based on the type of geometry we are tiling over.
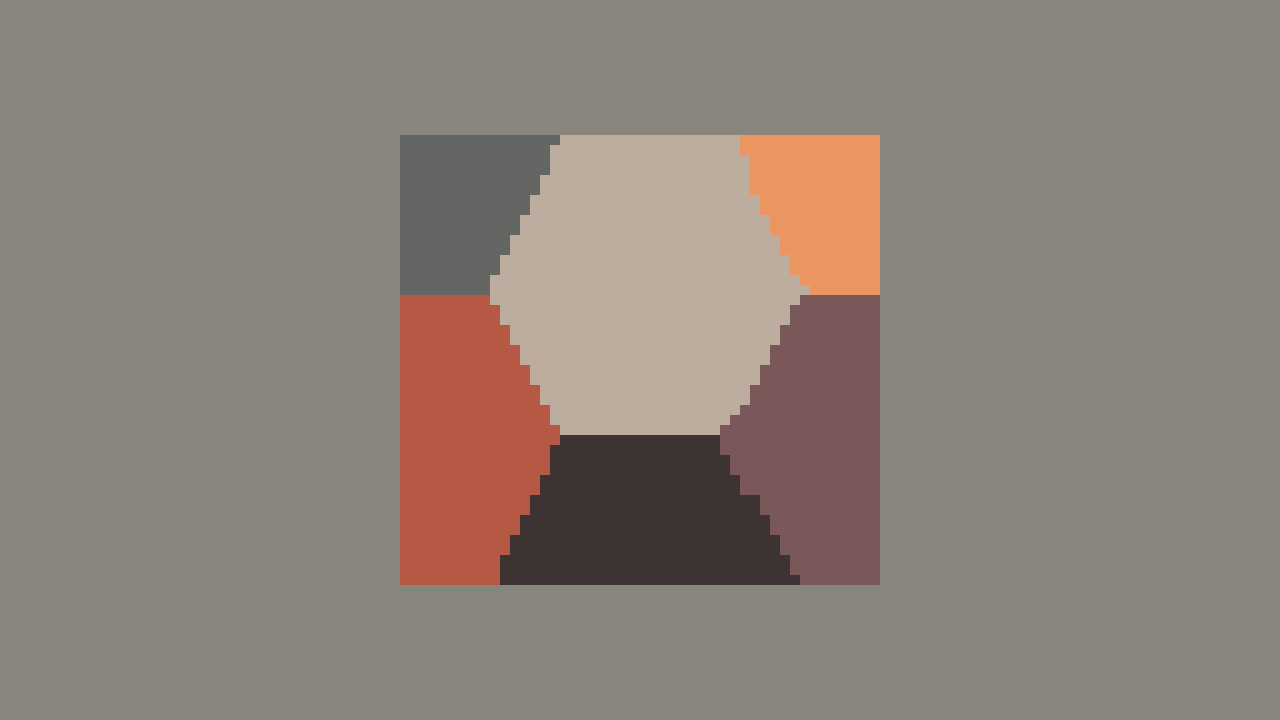
Above is a visualization of the reference image being tiled across
the screen. We can also move it into a monochromatic colour space to
make it easier to include other coincidental indexable shapes, as seen
below. Note that for this visualization the red channel increments in
steps of 30 (in 256 representation of 8bit), in reality the
step could be 1, to make indexing easier.
Normal axis aligned rectangle indexing can be used to map a cursor position to the hovered tile, with a slight adjustment for the staggered rows. The following description assumes that mx and my have already been moved into game space if you’re using a camera.
- Determine the y position of the tile. Divide the position by the height of the reference image and floor the result. To make the value one indexed add 1.
- Determine if the row is staggered. If so define an offset one half the width of the tile.
- Determine the x position the same way you did for the y, but subtract the offset if its an odd row.
(fn mouse->tile [mx my]
(let [ty (-> my (/ reference-image-height) (math.floor) (+ 1))
;; if the row is odd shift the tile to the left by a half width
odd-offset (-> ty (% 2) (* (/ reference-image-width 2)))
tx (-> mx (- odd-offset) (/ reference-image-width) (math.floor) (+ 1))]
(values tx ty)))
In addition to knowing what hexagon we are over in the hexgrid, it may also be useful to know what part of the hexagon we are in. In the example below the hexagons are broken into 6 sextants (referred to as angles for the rest of this post).

Using the green channel ensures that the signal is independent of the channel used for indexing the hex grid itself and makes it easy to combine the two reference images, as shown below.
There is still a lot of space available in the reference image to represent other aspects of the hexagon. For example, we could use the blue channel to indicate where the middle of the hexgrid is and where the outline is.

With love2d you can use ImageData:getPixel to get the
colour value of the reference image at point x y. In our example the red
channel maps to the hexagon index and the green channel maps to the
angle of the hexagon.
(local reference-image (love.image.newImageData :hexagon-reference-image.png))
(fn xy->reference-image-index [x y]
(let [(r g _b _a) (reference-image:getPixel x y)
index r
angle g]
(values index angle)))If you’re using another library or engine you can use their equivalent, or convert the image into a data array to be indexed directly.
Note the x y values above are the position relative to the top right of the reference image. To transform the mouse position to the reference image space you can subtract it’s top left corner from the cursor position.
(fn cursor->reference-image-info [mx my tx ty]
[t (* ty reference-image-height)
odd-offset (-> ty (% 2) (* (/ reference-image-width)))
l (-> tx (* reference-image-width) (- odd-offset))
(index angle) (xy->reference-image-index (- mx l) (- my t))]
(values index angle))Describing the Hexgrid
For the purpose of this post I am working with flat topped hexagons in a euclidean grid that have an ascended offset, i.e. the odd columns and rows are staggered upward and rightward.
The tiled references images are also staggered, with odd rows (assuming row and column counts start at 1) being shifted to the left by half their width.
Due to these offsets the indexing parameters for the even and odd rows are different.
When describing the position of the hexagon within the reference image we will follow the convention that the top left be 1 and the bottom right be 6.

By identifying the position of the first hexagon in the reference image, the other position of the other hexagons can be determined by their relative position.
Looking at the odd rows we can make a few observations:
- In the x axis, Hexagon 1 follows the pattern [0, 2, 4, 6].
- In the y axis, Hexagon 1 follows the pattern [1, 4, 7, 10].
(fn odd-tile->hexgrid-position [tx ty]
(values (-> tx (- 1) (* 2))
(-> ty (- 1) (* 3) (+ 1))))Looking at the even rows we can make a few observations:
- In the x axis, Hexagon 1 follows the pattern [1, 3, 5, 7].
- In the y axis, Hexagon 1 follows the pattern [2, 5, 8, 11].
(fn even-tile->hexgrid-position [tx ty]
(values (-> tx (- 1) (* 2) (+ 1))
(-> ty (- 2) (* 3) (+ 2))))Using the above observations to identify the absolute position of
Hexagon 1, an indexable table of relative offsets for all hexagons in
the reference image would look like
[[0 0] [1 1] [2 0] [0 1] [1 2] [2 1]] for both the even and
odd rows.
(fn cursor->hexgrid-position [mx my]
(let [(tx ty) (mouse->tile mx my)
offset-index [[0 0] [1 1] [2 0] [0 1] [1 2] [2 1]]
(index angle) (cursor->reference-image-info mx my tx ty)
[ox oy] (. offset-index angle)
tiling-index-function (if (-> ty (% 2) (= 0))
even-tile->hexgrid-position
odd-tile->hexgrid-position)
(h1-x h1-y) (tiling-index-function tx ty)]
(values (+ h1-x ox) (+ h1-y oy) angle)))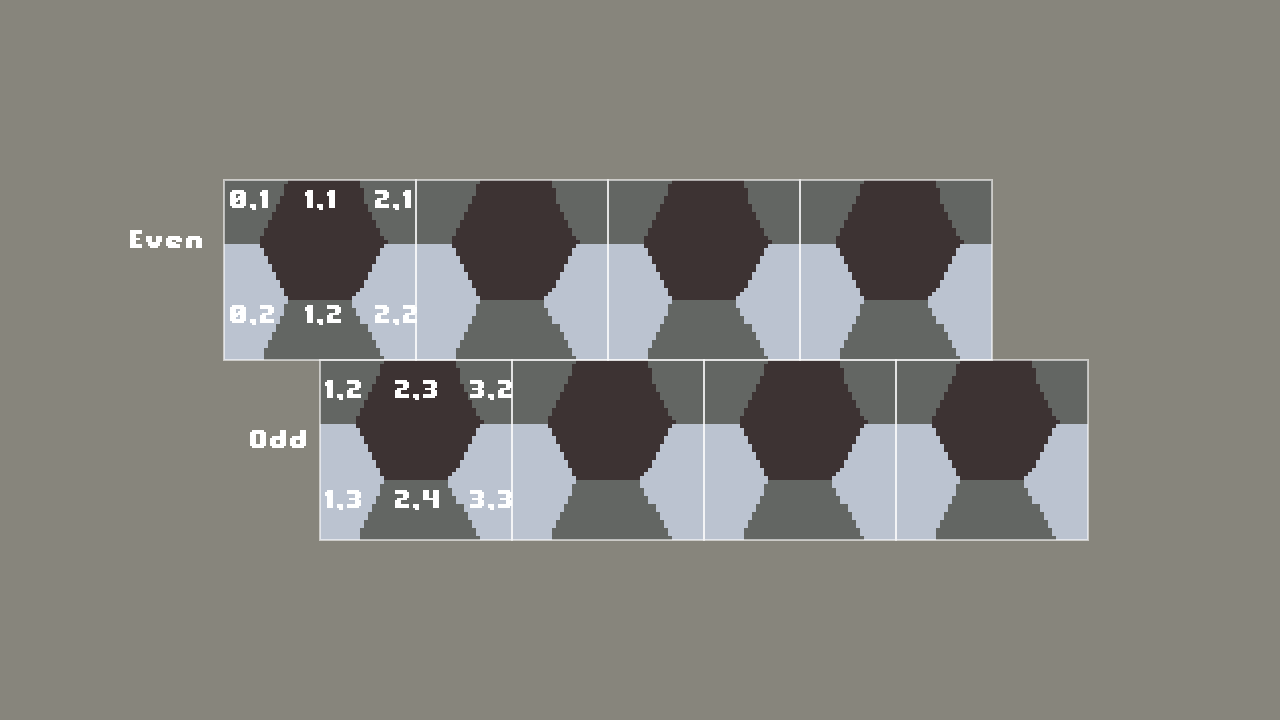
Closing
You should now be able to map your cursors position to a specific irregular hexagon, getting its position and the angle that your mouse is over.
This approach lets you customize how you index a subset of a grid and can be generalized for other irregular but periodically repeating shapes.
If you are working with regular hexagons, I’d recommend you stick with the Red Blog Games approach. This approach is best suited for pixel based hexagon.